Finally, to obtain the summary of map we compose the previous results as fol- lows. MaxLive for map is the sum of the corresponding Esc for all lines plus the the maximum MaxLive of all lines but discounting the corresponding Esc:

MaxLivemap = MaxLivel − Escl + Escl l∈{1,2,5,6} l∈{1,2,5,6} = ⊔ {1 − 1, 1 − 1, list size + 2 − list size, list size − list size} +(1+1+list size+list size) =2+(2+2×list size)=2×list size+4

Esc of map should count all objects that (may) escape from map. From all objects accounted for in Escl, for l ∈ {1, 2, 5, 6}, only the iterator allocated at line 2 is captured by map. All other objects escape. Thus, we get:

Escmap = Esc1 + Esc5 + Esc6 = 1 + list size + list size = 2×list size+1 

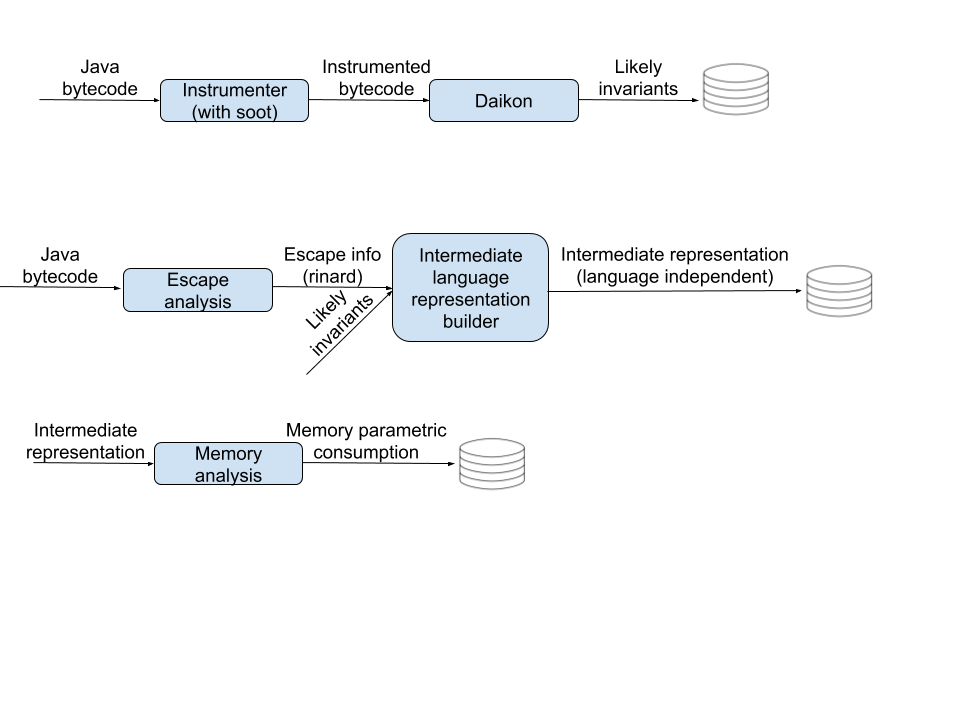
Buw how are the invariants obtained? They are generated using a tool called Daikon that generates likely pre- and post-conditions of method. We add calls to dummy methods right next to relevant lines inside a loop. The parameters of these dummy methods must be the variables which will have a part in the invariant. They are obtained with an enriched live variable analysis. Moreover, one has to distinguish between variables that are involved in the invariant, and what we may call inductive variables, i.e., the variables that change values with each loop iteration.

For example, consider the following code:

void m(int p){
          for(int i=1; i < p; i++){
              Integer temp = new Integer(i);
              m2(temp);
          }
        }

Suppose we want to analyze how many times m2 is executed. The live variables at that program point are temp, i and p. So we insert a call to a dummy method with those parameters:

void m(int p){
          for(int i=1; i < p; i++){
              Integer temp = new Integer(i);
              
              DummyClass.method1(temp,i,p);
              m2(temp);
          }
        }

When daikon generates preconditions for the method, it will include as a result that 1≤i≤p. So the parametric invariant is that the parameter is p, there exist some variable temp and some variable i such that 1≤i≤p. However, we must only count on i, not on temp, as temp isn't inductive. The notation used for the invariant results in this: [p] -> {[i] -> ∃ temp : 1≤i and i≤p} (you might think of it as a parametric set and what's happening is that we want to count the parametric number of elements of the set).

The Java code is converted into an intermediate representation equivalent to the one described in section 4 of the paper. More specifically, it is a languange independent representation of the callgraph, enriched with:

a) Likely invariants of all objects created and methods called

b) Which objects escape each method (it's context sensitive).

After this, we build the memory consumption only using the intermediate represention. The process is described in this paper (link). This makes it easier for us to analyze programs written in other languages, as the cost reduces to write the intermediate representation.

For more details, check the README located in the github repository.